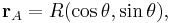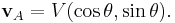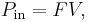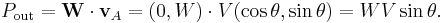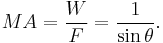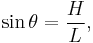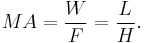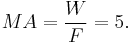Inclined plane

Inclined Plane

The Johnstown Inclined Plane in Johnstown, Pennsylvania.
Classification Simple machine
Industry Construction

An inclined plane is a straight ramp that is cut into a hillside and used for moving loads up and down the hill. Often the inclined plane was provided with cars riding on rails and pulled up and lowered down using a cable drive system powered by a steam engine. An example is the Johnstown Inclined Plane which was built in the late 1800's.

Renaissance scientists added the inclined plane to the five of simple machines described by Hero of Alexandria.[1] It is a flat surface that lies at an angle relative to level ground used to form a ramp to raise and lower a load. The force required to lift the load is reduced by pulling it up the ramp.

Assuming the movement of the load does not dissipate or store energy, the mechanical advantage of an inclined plane is the ratio of the length of the ramp to the height lifted.[2] [3]

Contents

Ramps and screws

An inclined plane is one of the six simple machines identified by Renaissance scientists. The inclined plane is a ramp that assists moving heavy objects up and down heights.

Portable ramps allow easy loading and unloading of high-decked trucks. Siege ramps gave ancient armies the ability to bring war machines to the top of fortress walls. slides allow fragile objects, including humans, to be rapidly and safely lowered down a vertical rise by resisting gravitational force with the normal force provided by the stiff surface of the inclined plane. Airplane rescue slides allow people to rapidly and safely reach the ground from the height of a passenger airplane.

The screw is an inclined plane wrapped around a cylinder. The Archimedes screw has been used since ancient times to move a variety of materials such as water, minerals and grain.[4]

Mechanical advantage

The mechanical advantage of an inclined plane is the ratio of the weight of the load on the ramp to the force required to pull it up the ramp. If energy is not dissipated or stored in the movement of the load, then this mechanical advantage can be computed from the dimensions of the ramp.

In order to show this, let the position of a rail car A on along ramp be given by the coordinates

\mathbf{r}_A = R (\cos\theta, \sin\theta),

where R is the distance along the ramp. The velocity of the car up the ramp is given by

\mathbf{v}_A = V (\cos\theta, \sin\theta).

Because there are no losses, the power used by F to move the load up the ramp equals the power out, which is the vertical lift of the weight W of the load.

The input power pulling the car up the ramp is given by

P_{\mathrm{in}} = FV,\!

and the power out is

P_{\mathrm{out}} = \mathbf{W}\cdot\mathbf{v}_A = (0, W)\cdot V (\cos\theta, \sin\theta) = WV\sin\theta.

Equate the power in to the power out to obtain the mechanical advantage as

MA = \frac{W}{F} = \frac{1}{\sin\theta}.

The mechanical advantage of an inclined can also be calculated from the ratio of length of the ramp L to its height H, because the sine of the angle of the ramp is given by

\sin\theta = \frac{H}{L},

therefore,

MA = \frac{W}{F} = \frac{L}{H}.

Example: If the height of a ramp is H = 1 meter and its length is L = 5 meters, then the mechanical advantage is

MA = \frac{W}{F} = 5.

See also

External links

References

  1. ^ Usher, Abbott Payson (1988). A History of Mechanical Inventions. USA: Courier Dover Publications. pp. 98. ISBN 048625593X. http://books.google.com/books?id=xuDDqqa8FlwC&pg=PA196#v=snippet&q=wedge%20and%20screw&f=false. 
  2. ^ Prater, Edward L. (1994). "Basic Machines". Naval Education and Training Professional Development and Technology Center, NAVEDTRA 14037. http://www.constructionknowledge.net/public_domain_documents/Div_1_General/Basic_Skills/Basic%20Machines%20NAVEDTRA%2014037%201994.pdf. 
  3. ^ Bureau of Naval Personnel (1971). "Basic Machines and How They Work". Dover Publications. http://www.webpal.org/SAFE/aaarecovery/5_simple_technology/basic_machines.pdf. 
  4. ^ Mays, L. (2010). Ancient Water Technologies (illustrated ed.). Springer. pp. 16. ISBN 9789048186310. http://books.google.com/books?id=AEzOzSZEAToC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q=water%20screw&f=false.